5. Affine Transformation

5.1. Affine Transformation

Affine Transformation (Affine Transformation or Affine Map) is a linear transformation from two-dimensional coordinates (x, y) to two-dimensional coordinates (u, v). Its mathematical expression is as follows:

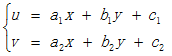
The corresponding homogeneous coordinate matrix representation is:

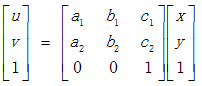
Affine transformation maintains the "straightness" (straight lines remain straight lines after affine transformation) and "parallelism" (the relative position relationship between straight lines remains unchanged, parallel lines remain parallel lines after affine transformation, and the position order of points on the straight lines does not change) of two-dimensional graphics. Three pairs of non-collinear corresponding points determine a unique affine transformation.

The rotation and stretching of an image is the image affine transformation. Affine transformation also requires an M matrix. However, since affine transformation is relatively complex, it is generally difficult to find this matrix directly. OpenCV provides an automatic solution to M based on the correspondence between the three points before and after the transformation. This function is

M=cv2.getAffineTransform(pos1,pos2), where the two positions are the corresponding positional relationship before and after the transformation. The output is the affine matrix M. Then use the function cv2.warpAffine().

two methods of image transformation cv2.warpAffine and cv2.warpPerspective

5.2. Actual effect display

Let's take the vertical transformation as an example to see how Python is written:

Code path:

/home/pi/project_demo/06.Open_source_cv_fundamentals_course/B.Geometric_Transformations/05_Affine_Transformation.ipynb

​x
import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('yahboom.jpg',1)

img_bgr2rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img_bgr2rgb)
plt.show()
# cv2.waitKey(0)

xxxxxxxxxx
imgInfo = img.shape
height = imgInfo[0]
width = imgInfo[1]
#src 3->dst 3 (左上角，左下角，右上角 Top left, bottom left, top right)
matSrc = np.float32([[0,0],[0,height-1],[width-1,0]])
matDst = np.float32([[50,50],[300,height-200],[width-300,100]])
#组合 combination
matAffine = cv2.getAffineTransform(matSrc,matDst)# mat 1 src 2 dst
dst = cv2.warpAffine(img,matAffine,(width,height))
img_bgr2rgb = cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)
plt.imshow(img_bgr2rgb)