1 PID algorithm theory

1.1 algorithm introduction

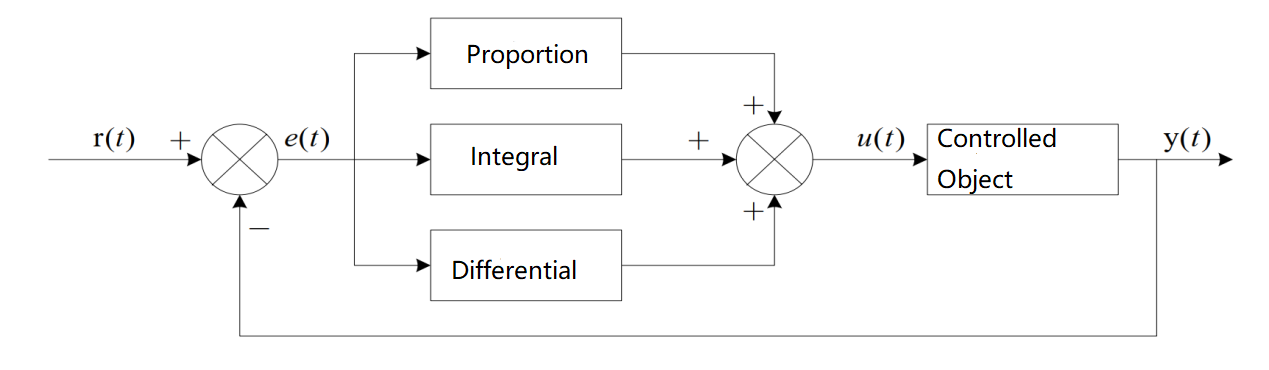
PID is to perform proportional, integral and derivative operations on the input deviation, and the superposition results of the operations are used to control the actuator. The formula is as follows:

$u(t)=K_p[e(t)+\frac{1}{T_i}\int_{0}^{t}e(t)dt+Td\frac{de(t)}{dt}]$

It consists of three parts:

• P is the ratio, which is the input deviation multiplied by a coefficient;
• I is the integral, which is the integral operation of the input deviation;
• D is the derivative, and the input deviation is differentiated.

The following figure shows a basic PID controller:

1.1.1 Scale part

The mathematical expression for the proportional part is: $K_p*e(t)$

In an analog PID controller, the role of the proportional link is to react instantaneously to deviations. Once the deviation occurs, the controller will immediately take control, so that the control amount changes in the direction of reducing the deviation. The strength of the control effect depends on the proportionality coefficient. The larger the proportionality coefficient, the stronger the control effect, the faster the transition process and the smaller the static deviation of the control process; however, the larger the proportionality factor, the easier it is to generate oscillations and destroy the stability of the system. sex. Therefore, the selection of case coefficients must be appropriate, so that the transition time is small, the static difference is small and stable.

Advantages: Adjust the open-loop proportional coefficient of the system, improve the steady-state accuracy of the system, reduce the inertia of the system, and speed up the response speed.

Disadvantage: Only use P controller, too large open-loop proportional coefficient will not only increase the overshoot of the system, but also make the stability margin of the system smaller or even unstable.

1.1.2 Integral part

The mathematical expression of the integral part is: $\frac{K_p}{T_i}\int_{0}^{t}e(t)dt$ The larger the integral constant, the weaker the accumulation effect of the integral. At this time, the system is in transition. No oscillation will occur; however, increasing the integral constant will slow down the process of eliminating static errors, and it will take longer to eliminate deviations, but it can reduce overshoot and improve system stability. When Ti is small, the integral effect is stronger, and oscillation may occur in the transition time of the system, but the time required to eliminate the deviation is short. Therefore, Ti must be determined according to the specific requirements of actual control.

Advantage: Eliminates steady-state errors.

Disadvantage: The addition of the integral controller will affect the stability of the system and reduce the stability margin of the system.

1.1.3 Differential part

The mathematical expression of the differential part is: $K_p*Td\frac{de(t)}{dt}$

The role of the differential link prevents the variation of the deviation. It is controlled according to the change trend(change speed) of the deviation. The faster the deviation changes, the greater the output of the differential controller, and can be corrected before the deviation becomes larger. The introduction of differential action will help to reduce overshoot, overcome oscillation and stabilize the system, especially for high-order systems, which speed up the tracking speed of the system. However, the function of the differential is very sensitive to the noise of the input signal. Generally, the differential is not used for those systems with large noise, or the input signal is filtered before the differential works. The action of the differential part is determined by the differential time constant Td. The larger the Td, the stronger the effect of suppressing the deviation change; the smaller the Td, the weaker the effect of resisting the deviation change. The differential part obviously has a great effect on system stability. Appropriate selection of the differential constant Td can optimize the differential action.

Advantages: Make the response speed of the system faster, reduce the overshoot, reduce the oscillation, and have a "prediction" effect on the dynamic process.

1.2 Selection of PID algorithm

Digital PID control algorithms can be divided into position PID and incremental PID control algorithms. So before we decide to choose which PID algorithm to use, we should first understand its principle:

1.2.1 Position PID algorithm

$u(k)=K_pe(k)+K_I\sum_{i=o}e(i)+K_D[e(k)-e(k-1)]$

e(k): the value set by the user(target value) - the current state value of the control object

Proportion P : e(k)

Integral I : Accumulation of ∑e(i) errors

Differential D : e(k) - e(k-1) this time error - last time error

That is, the position PID is the actual position of the current system, the deviation from the expected position you want to achieve, and PID control is performed.

Because there is an error integral ∑e(i), which is always accumulated, that is, the current output u(k) is related to all the past states, and the accumulated value of the error is used;(error e will have error accumulation), the output u(k) corresponds to the actual position of the actuator. Once the control output is wrong(the current state value of the control object has a problem), a large change in u(k) will cause a large change in the system and the positional PID will reach the integral term. When saturated, the error will still continue to accumulate under the integral action. Once the error starts to change in the reverse direction, the system needs a certain time to exit from the saturation region. Therefore, when u(k) reaches the maximum and minimum, the integral action should be stopped and the integral should be required. Limiting and output limiting So when using position PID, we generally use PD control directly

The positional PID is suitable for objects with no integral components in the actuator, such as the control of the upright and temperature control systems of the steering gear and the balance trolley

Advantages: Position PID is a non-recursive algorithm, which can directly control the actuator(such as the balance car), the value of u(k) and the actual position of the actuator(such as the current angle of the car) are in one-to-one correspondence, so Works well in objects with actuators without integral components

Disadvantages: Each output is related to the past state, e(k) must be accumulated during calculation, and the computational workload is large.

1.2.2 Incremental PID algorithm

$\Delta u(k)=u(k)-u(k-1)=K_P[e(k)-e(k-1)]+K_ie(k)+K_D[e(k)-2e(k-1)+e(k-2)]$

Proportion P : $e(k)-e(k-1)$ this time error - last time error

Integral I : $e(k)$ bias

Differential D : $e(k)-2e(k-1)+e(k-2)$ This time error-2*last error + last time error

Incremental PID can be well seen according to the formula, once KP, TI, TD are determined, as long as the deviation of the three measured values before and after is used, the control amount $\Delta u(k)$ corresponds to the increment of the position error in recent times, not the deviation from the actual position. There is no error accumulation. That is to say, accumulation is not required in incremental PID. The determination of the control increment $\Delta u(k)$ is only related to the last three sampling values, and it is easy to obtain a better control effect through weighted processing, and when a problem occurs in the system, the incremental method will not seriously affect the system. Work

Summary: Incremental PID is to increment the positional PID. At this time, the controller outputs the difference between the position values calculated at two adjacent sampling times, and the result obtained is an increment, that is, in the last control On the basis of the amount, you need to increase(negative value means decrease) the control amount.

advantage:

①The influence of malfunction is small, and the error data can be removed by the method of logical judgment if necessary.

②The impact of manual/automatic switching is small, which is convenient to realize disturbance-free switching. When the computer fails, the original value can still be maintained.

③ There is no need to accumulate in the formula. The determination of the control increment Δu(k) is only related to the last three sampling values.

shortcoming:

① The integral truncation effect is large, and there is a steady-state error;

②The influence of overflow is great. For some controlled objects, it is not very good to use the incremental method;

1.2.3 the difference between incremental and positional

(1) The incremental algorithm does not need to do accumulation, the determination of the control amount increment is only related to the recent deviation sampling values, and the calculation error has little influence on the control amount calculation. The positional algorithm uses the accumulated value of past deviations, which is prone to large accumulated errors.

(2) The incremental algorithm obtains the increment of the control quantity. For example, in the valve control, only the change part of the valve opening is output, and the influence of misoperation is small. If necessary, the output can be limited or prohibited by logical judgment., will not seriously affect the work of the system. The positional output directly corresponds to the output of the object, so it has a greater impact on the system.

(3) The output of incremental PID control is the increment of the control amount, and there is no integral action, so this method is suitable for objects with integral components of the actuator, such as stepper motors, etc., while the positional PID is suitable for the actuator without Objects that integrate components, such as electrohydraulic servo valves.

(4) When performing PID control, the positional PID needs to have integral limiter and output limiter, while the incremental PID only needs to output the limiter

Positional PID and incremental PID are just two implementations of digital PID control algorithms, and they are essentially the same. The main difference is that the integral items are stored in different ways. The positional PID integral items are stored separately, and the incremental PID integral items are stored as part of the output. Various players on the Internet also have their own unique opinions on the use of positional and incremental. Opinion, it depends on which algorithm is suitable for our specific application scenario.

1.3 Debugging of PID parameters

There are many methods for PID controller parameter selection, such as trial and error method, critical proportionality method, and extended critical proportionality method. However, for PID control, the selection of parameters is always a very complicated task, which requires continuous adjustment to obtain a more satisfactory control effect. Based on experience, the general steps for PID parameter determination are as follows:

1.3.1 Determine the proportional coefficient Kp

When determining the proportional coefficient Kp, first remove the integral term and differential term of the PID, so that Ti=0 and Td=0, making it a pure proportional adjustment. The input is set to 60% to 70% of the maximum allowable output of the system, and the proportional coefficient Kp gradually increases from 0 until the system oscillates; and vice versa, the proportional coefficient Kp decreases gradually from this time until the system oscillation disappears. Record the proportional coefficient Kp at this time, and set the proportional coefficient Kp of the PID to be 60% to 70% of the current value.

1.3.2 Determine the integral time constant Ti

After the proportional coefficient Kp is determined, set a larger integral time constant Ti, and then gradually decrease Ti until the system oscillates, and then reversely increase Ti until the system oscillation disappears. Record the Ti at this time, and set the integral time constant Ti of the PID to be 150% to 180% of the current value.

1.3.3 Determine the differential time constant Td

Differential time constant Td generally does not need to be set, it can be set to 0. At this time, PID adjustment is converted into PI adjustment. If it needs to be set, it is the same as the method for determining Kp, taking 30% of its value when it is not oscillating.

1.3.4 System no-load and on-load joint debugging

Fine-tune the PID parameters until the performance requirements are met.

Of course, this is just my personal debugging method, which is not necessarily suitable for everyone and every environment. It is only provided for your reference; however, there are also classic PID debugging formulas circulating on the Internet, and I also post them for your reference:

Parameter tuning to find the best, in order from small to large.

First proportional, then integral, and finally add the differential.

The curve oscillates very frequently, and the proportional dial should be enlarged.

The curve floats around the big bend, and the proportional dial turns to the small turn.

When the curve deviates, the recovery is slow, and the integration time decreases.

The curve fluctuation period is longer, and the integration time is longer.

The oscillation frequency of the curve is fast, so reduce the differential first.

If the momentary difference is large, the fluctuation will be slow, and the differentiation time should be lengthened.

The ideal curve has two waves, with the front high and the back low four to one.

One look at the second adjustment and more analysis, the adjustment quality will not be low.

PID is proportional(P), integral(I), and differential(D) control algorithms. It is not necessary to have these three algorithms at the same time. It can also be PD, PI, or even only P algorithm control. One of the simplest ideas for closed-loop control I used to have was only P control. The current result is fed back and subtracted from the target. If it is positive, it will decelerate, and if it is negative, it will accelerate. Of course, this is just the simplest closed-loop control algorithm, that is, go back to the positional and incremental summary in the previous section. For details, please refer to our current control environment. Because of the differences of each control system, the parameters that can make our system achieve the most stable effect are of course OK.